M203 20251213 Conics_Maxima, Minima of Quadratics_Circles_Ellipses_Hyperbolas
2 . Maxima and Minima of Quadratics
1 ) $f(x)=x^2+6x+5$. Find the smallest possible value of $f(x)$.
2 ) Let $f(x)=ax^2+bx+c$, where $a,b,c$ are real numbers and $a>0$. In terms of $a,b$ and $c$, find the real value of $x$ that makes $f(x)$ as small as possible. What happens if $a$ is negative?
好的,这是从图片中提取的数学公式,都用 $\$$ 符号包围,方便您粘贴到 Obsidian 笔记中。
- $f(x) = ax^2 + bx + c$
- $= a(x^2 + \frac{b}{a}x + (\frac{b}{2a})^2) + c - a(\frac{b}{2a})^2$
- $= a(x + \frac{b}{2a})^2 + c - \frac{b^2}{4a}$
- 顶点坐标 (Vertex):$(-\frac{b}{2a}, c - \frac{b^2}{4a})$
- 顶点公式 (Vertex formula) - x 坐标:$x = -\frac{b}{2a}$
- $f(x) = ax^2 + bx + c$
- $= a(x^2 + \dfrac{b}{a}x + (\dfrac{b}{2a})^2) + c - a(\dfrac{b}{2a})^2$
- $= a(x + \dfrac{b}{2a})^2 + c - \dfrac{b^2}{4a}$
- 顶点坐标 (Vertex):$(-\dfrac{b}{2a}, c - \dfrac{b^2}{4a})$
- 顶点公式 (Vertex formula) - x 坐标:$x = -\dfrac{b}{2a}$
3 ) Let $k$ be a real number. Find the minimum possible distance between $k(1+3i)$ and $2i$ in the complex plane.

7 ) A) Find the minimum value of $p(y)=2y^2-4y+19$
B) Find the maximum value of $37-16r-r^2$
6 ) Suppose the temperature of each point $(x,y)$ in the plane is given by the function $x^2+y^2-4x+6y$. Find the coldest point in the plane and determine its temperature.

Answer: -13 Celsius temperature
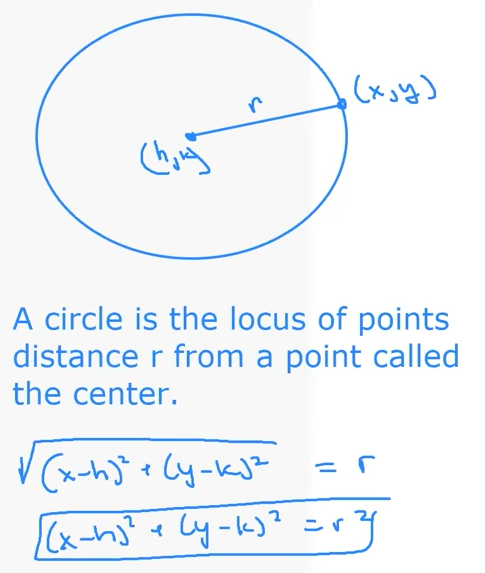
3 . Circles
Equation: $(x-h)^2 + (y – k)^2 = r^2$ with center $(h,k)$ and radius $r$.
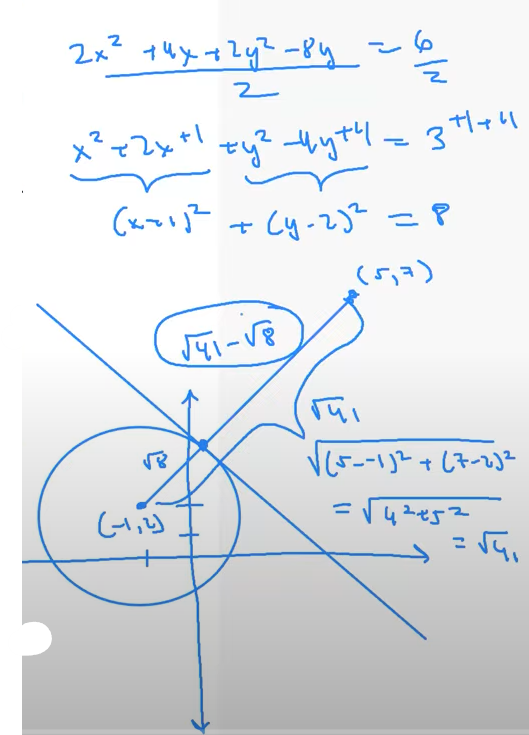
1 . Find the distance from $(5,7)$ to the nearest point on the graph of $2x^2+4x +2y^2 – 8y = 6$
4 . Find an equation whose graph is a circle that has a diameter with endpoints $(3,2)$ and $(7,-4)$.
$center: (5,-1)$ $r= \sqrt{2^2+3^2} = \sqrt{13}$
9 . The circumcircle of a triangle is the circle that passes through all three vertices of the triangle. Find an equation whose graph is the circumcircle of a triangle with vertices $(-2,5)(-4,-3)(0,-3)$
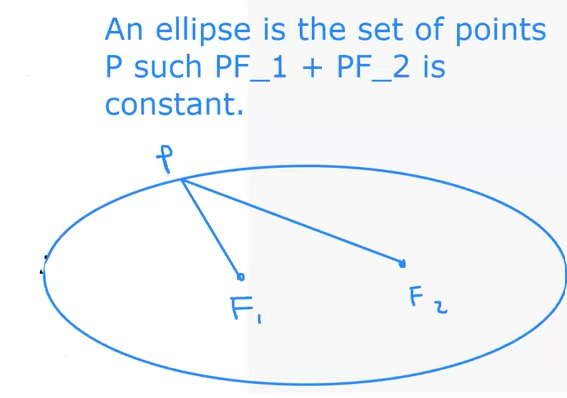
4 . Ellipse
- The defining property is $PF_1 + PF_2 = 2a$, where $2a$ is the constant distance.
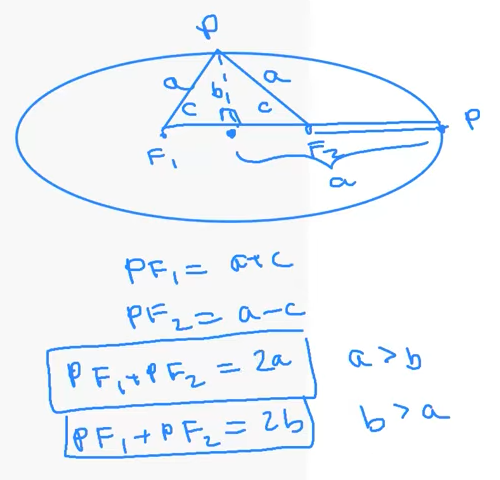
- If the ellipse passes through $(a, 0)$ and $(0, b)$, the equation is: $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$
- $2a$ is the length of the major axis, and $2b$ is the length of the minor axis.
4. Standard Equation (Center at $(h, k)$): Suppose that the ellipse has $(h, k)$ as its center, $(h+c, k)$ as a focus (assuming a horizontal major axis), and a major axis of length $2a$.
- The relationship between the major axis, minor axis, and distance to the focus is given by: $b^2 = a^2 - c^2$
- The equation in Standard Form is:
$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$
5. Relationship between Axes and Foci:
- (major axis length)$^2$ = (minor axis length)$^2$ + (distance between foci)$^2$.
- This means:$(2a)^2 = (2b)^2 + (2c)^2$
- Dividing by 4 yields the fundamental relationship:
$a^2 = b^2 + c^2$
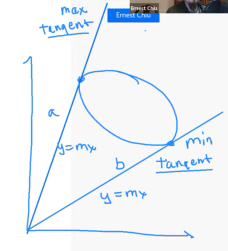
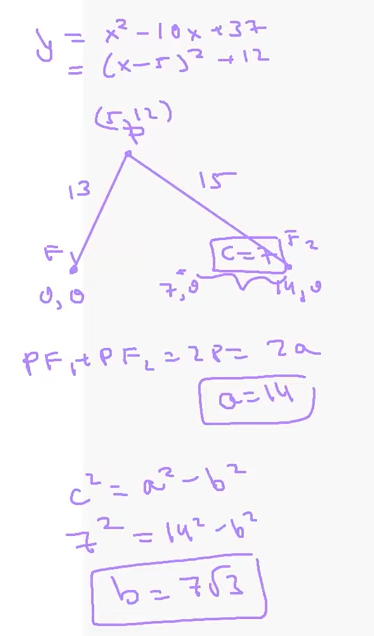
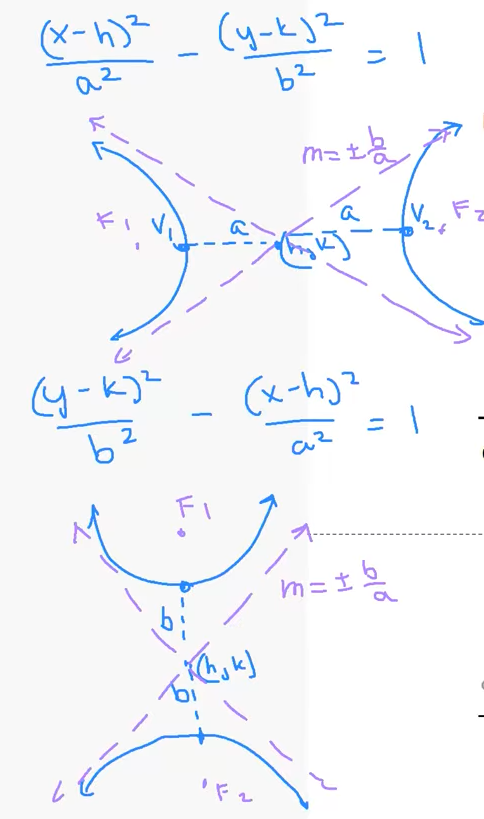
1 ) Consider the graph of the equation $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}$ = 1. What does the graph look like when $a=b, a>b, a 2 ) Graph each of the following ellipses below, and find an equation that produces the given graph. Find the center, foci and the lengths of both axes of each ellipse. a. The center is $(4, -2)$, the major axis is horizontal with length $6$, and $(4, -3)$ is one endpoint of the minor axis. 3 ) Find the center, foci, and the lengths of both axes of each graph. a. $\dfrac{(x-1)^2}{16} + \dfrac{(y+7)^2}{25} =1$ 7 ) An ellipse has foci (0, 0) and (14, 0) and passes through the vertex of the parabola with equation $y = x^2 – 10x + 37$. Find the length of the major and minor axis of this ellipse and the distance of foci. Definition: 1. Suppose we have points $F_1$, $F_2$ in a plane. For any positive constant $k$, the locus of all points $P$ in the plane such that $|PF_1 - PF_2| = k$ is called a hyperbola. A hyperbola consists of two pieces that are called branches of the hyperbola. $F_1$, $F_2$ are the foci of the hyperbola. The line connecting the foci meets the hyperbola at the vertices of the hyperbola. The midpoint of the segment connecting a hyperbola’s vertices is the hyperbola’s center. 2. The hyperbola has foci $F_1(c, 0)$ and $F_2(-c, 0)$ and vertices $V_1(a, 0)$ and $V_2(-a, 0)$, where $a$ and $c$ are positive constants with $c > a$. Let $P(x, y)$ be a point on the hyperbola. The equation of the hyperbola is $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$ where $b^2 = c^2 - a^2$. 3. We call a line an asymptote of a graph if the graph gets closer and closer to, but does not intersect, the line as $x$ and/or $y$ gets far from $0$. For the hyperbola $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$, the asymptotes are given by $\dfrac{x}{a} = \pm \dfrac{y}{b}$ A hyperbola is the locus of points P such that $|PF_1 - PF_2|$ is a constant. $c^2=a^2+b^2$ 1 ) Graph the equation $\dfrac{x^2}{9} - \dfrac{y^2}{4} = 1$. Find the vertex, foci. Graph the equation $\dfrac{y^2}{9} - \dfrac{x^2}{4} = 1$. Find the vertex, foci. 5 ) Graph the following equations: $xy = 1$ 7 ) The graph of $2x^2+xy+3y^2-11x-20y+40=0$ is an ellipse in the first quadrant of the $xy$-plane. Let $a$ and $b$ be the maximum and minimum values of $y/x$ over all points $(x, y)$ on the ellipse. What is the value of $a+b$? To find the maximum and minimum values of $\frac{y}{x}$, we interpret $k = \frac{y}{x}$ as the slope of a line passing through the origin $(0,0)$ and a point $(x, y)$ on the ellipse. The values $a$ and $b$ correspond to the slopes of the two lines through the origin that are tangent to the ellipse. Substitute $y = kx$ into the given equation $2x^2 + xy + 3y^2 - 11x - 20y + 40 = 0$: $$2x^2 + x(kx) + 3(kx)^2 - 11x - 20(kx) + 40 = 0$$ Rearrange the terms as a quadratic equation in $x$: $$(3k^2 + k + 2)x^2 - (20k + 11)x + 40 = 0$$ For the line to be tangent to the ellipse, this quadratic equation must have exactly one real solution for $x$. Therefore, the discriminant $D$ (or $\Delta$) must be zero: $$D = [-(20k + 11)]^2 - 4(3k^2 + k + 2)(40) = 0$$ Expanding the terms: $$(400k^2 + 440k + 121) - 160(3k^2 + k + 2) = 0$$ $$400k^2 + 440k + 121 - 480k^2 - 160k - 320 = 0$$ $$-80k^2 + 280k - 199 = 0$$ Which simplifies to: $$80k^2 - 280k + 199 = 0$$ The roots of this quadratic equation are $a$ and $b$. According to Vieta's Formulas, for any quadratic $Ak^2 + Bk + C = 0$, the sum of the roots is given by: $$a + b = -\frac{B}{A}$$ Plugging in our values ($A = 80, B = -280$): $$a + b = -\frac{-280}{80} = \frac{280}{80} = \frac{7}{2}$$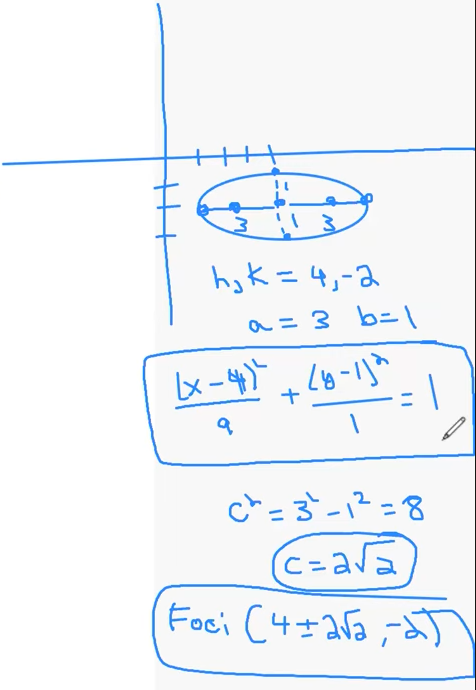
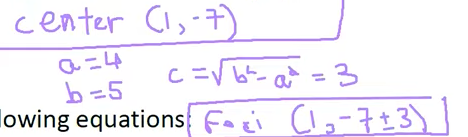
5 . Hyperbolas
6 . Challenging Problems
1. Substitute $y = kx$
2. Set the Discriminant to Zero
3. Apply Vieta's Formulas